Рішення лінійних Систем Рівнянь: Прямий і Ітераційний вирішувач

1. Лінійна Статична Завдання Кінцевих Елементів
2. прямі методи
3. ітераційні методи
4. Основні Висновки по Прямим і ітераційних методів Рішення

У цій статті блогу ми представимо два класи алгоритмів, які використовуються в COMSOL для вирішення систем лінійних рівнянь, що виникають при вирішенні будь-якої задачі кінцевих елементів. Така інформація є суттєвою для розуміння, як внутрішніх алгоритмів роботи решателя (обчислювальної програми), так і зростаючих вимог до пам'яті через кількісного ускладнення завдання.

Лінійна Статична Завдання Кінцевих Елементів

Розглянемо лінійну статичну задачу кінцевих елементів, складену з трьох вузлів і трьох елементів:

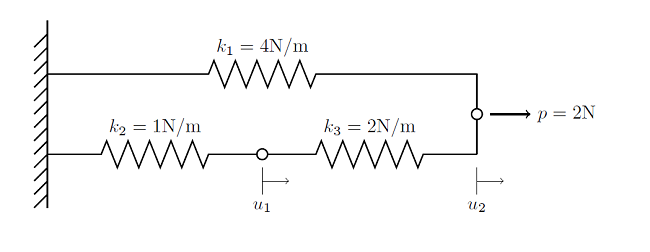
Кожен елемент обмежений двома вузлами. Один з вузлів знаходиться на жорсткій стінці, де, як відомо, зсув дорівнює нулю і немає необхідності вирішувати рівняння для цього вузла. Також як в попередній статті блогу по лінійним статичним завданням кінцевих елементів , Ми можемо записати рівняння балансу сил для кожного вузла:

f_ {u_1} = k_3 (u_2-u_1) -k_2 (u_1-0)

f_ {u_2} = p-k_3 (u_2-u_1) -k_1 (u_2-0)

можна записати їх також у вигляді:

\ Begin {Bmatrix} f_ {u_1} \\ f_ {u_2} \ end {Bmatrix} = \ begin {Bmatrix} 0 \\ p \ end {Bmatrix} - \ begin {bmatrix} k_2 + k_3 && -k_3 \\ - k_3 && k_1 + k_3 \ end {bmatrix} \ begin {Bmatrix} u_1 \\ u_2 \ end {Bmatrix}

або навіть в більш компактній формі:

\ Bf {f (u) = b-Ku}

Ми можемо вирішити це завдання за допомогою ітераційного методу Ньютона-Рафсона і, оскільки завдання є лінійної і статичної з початковим значенням \ mathbf {u} _ {init} = \ mathbf {0}, рішення буде знайдено за одну ітерацію:

\ Mathbf {u} _ {solution} = \ mathbf {K ^ {- 1} b}

Далі, в цьому завданні є тільки два невідомих, або ступеня свободи (degrees of freedom - DOF), і вона може бути легко вирішена за допомогою ручки і паперу. Але в загальному випадку, ваші матриці будуть нараховувати від тисяч до мільйона DOF's, і знаходження рішення вищевказаного матричного рівняння є найбільш вимогливою, в обчислювальному сенсі, частиною завдання. При вирішенні таких систем лінійних рівнянь на комп'ютері, слід також мати поняття про числі обумовленості , - міру чутливості рішення до зміни вхідних даних. Хоча в середовищі COMSOL, число обумовленості ніколи безпосередньо не обчислюється (так як по тимчасових витратах це можна порівняти з рішенням самого завдання), ми будемо говорити про нього в відносному вираженні. Це число грає важливу роль в чисельних методах, використовуваних при вирішенні систем лінійних рівнянь.

Існують два основних (фундаментальних) класу алгоритмів, використовуваних для вирішення \ bf {K ^ {- 1} b}: прямі та ітераційні методи. Ми представимо обидві групи цих методів і розглянемо їх загальні властивості і відносну ефективність, нижче.

прямі методи

Вирішувачі прямих методів, що використовуються в COMSOL - це MUMPS , PARDISO , і SPOOLES вирішувачі. Всі вони використовують метод LU-розкладання , Також званої LU-факторизації.

Всі ці вирішувачі дають одне і те ж рішення для всіх коректно-поставлених завдань кінцевих елементів, у вирішенні яких вони володіють найбільшою перевагою. Вони навіть можуть вирішувати деякі некоректні завдання. З точки зору вирішення, неважливо який саме вирішувач ви виберете, так як всі вони знайдуть одне і те ж рішення. Прямі вирішувачі відрізняються тільки по своїй відносній швидкості виконання. Кожен з MUMPS, PARDISO, і SPOOLES решателей може скористатися перевагами всіх ядер процесора на одній машині, але PARDISO буде трохи швидше, а SPOOLES трохи повільніше інших прямих решателей. При цьому, однак, SPOOLES використовує найменшу кількість пам'яті. Всі прямі вирішувачі вимагають масу оперативної пам'яті RAM, але MUMPS і PARDISO можуть зберігати рішення поза ядра, що означає, що вони можуть використовувати при вирішенні деяких завдань жорсткий диск (створюють файл-підкачки). Вирішувач MUMPS підтримує також кластерні обчислення, що дозволяють використовувати більший обсяг пам'яті, ніж наданий єдиною машиною.

Якщо ви займаєтеся вирішенням завдання, яка не має рішення (наприклад, конструкційна завдання з необмеженою навантаженням), прямі вирішувачі все одно спробують вирішити задачу, але, швидше за все, видадуть повідомлення про помилку подібне до цього:

Failed to find a solution. The relative residual (0.06) is greater than the relative tolerance. Returned solution is not converged.

Якщо ви отримали такого типу повідомлення про помилку, тоді необхідно все перевірити ще раз, щоб переконатися, що завдання поставлене коректно.

ітераційні методи

Ітераційні вирішувачі в середовищі COMSOL охоплюють безліч різних підходів, але всі вони концептуально досить прості для розуміння, будучи по суті подібні Метод сполучених градієнтів . До інших методів відносяться generalized minimum residual method (узагальнений метод мінімальних нев'язок) і Стабілізований метод бісопряжённих градієнтів , І безліч їх варіацій, але всі вони ведуть себе подібним чином.

На відміну від прямих решателей, ітераційні методи наближаються до рішення поступово, більш ніж за один обчислювальний крок. Отже, при вирішенні завдання ітераційним способом, можна спостерігати за зменшенням оціночної помилки рішення з ростом числа ітерацій. Для добре-обумовлених завдань, збіжність буде рівномірно монотонної. Якщо ви маєте справу з завданням не (досить) добре-обумовленої, тоді збіжність буде повільніше. Осциляційного поведінку итерационного решателя часто сигналізує про те, що завдання не коректно поставлена, наприклад, коли завдання є недостатньо обмеженою. Типовий графік збіжності для ітераційного решателя наведено на малюнку нижче:

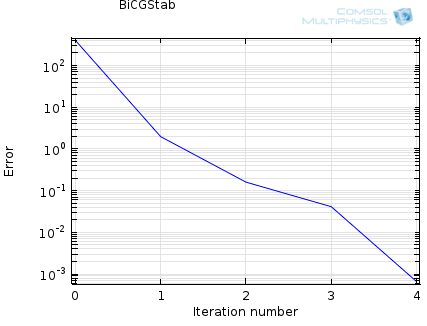
За замовчуванням, модель вважається що зійшли, коли оцінка помилки (рішення) в ітераційне вирішувача стає менше ніж 10-3. Цей параметр контролюється в вікні Налаштування розв'язувача:

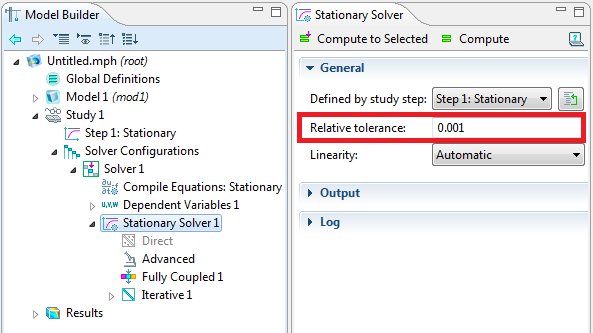
Ця похибка може бути слабшим (менше по порядку величини) для більш швидкого вирішення, або жорсткіше, для кращої точності на поточній сітці розбиття. Похибка завжди повинна бути більше машинної точності представлення чисел (2.22 × 10-16) і числа обумовленості (яке залежить від завдання). В принципі, немає сенсу робити вимога до похибки надмірно жорстким, так як вхідні дані у вашій моделі, найчастіше, визначені з точністю до другого знака після коми. Якщо ви все-таки вирішите змінити відносну похибку, ми наполегливо рекомендуємо не змінювати її більш ніж на порядок в порівнянні з рішенням. Пам'ятайте, що ви знайдете рішення з меншою похибкою тільки для поточного розбиття сітки і, часто, більш ефективним рішенням буде подрібнення сітки.

Великою перевагою ітераційних методів є використання ними пам'яті, яке значно менше, ніж у прямих решателей при вирішенні завдань такої ж розмірності (числа рівнянь). Істотним недоліком є ​​те, що ітераційні вирішувачі не завжди «просто працюють». Різна фізика вимагає різних налаштувань итерационного решателя в залежності від природи вирішуваних рівнянь.

На щастя, в середовищі COMSOL вже є вбудовані за замовчуванням решателя для будь-якої фізичної задачі. COMSOL автоматично визначить розділ фізики розв'язуваної задачі, а також її розмір, і підбере вирішувач - прямий або ітераційний - для цього випадку. За замовчуванням, ітераційні вирішувачі вибираються, виходячи з вимог найкращої точності і найменшою використовуваної пам'яті, і не вимагають ніякого втручання з боку користувача для своєї настройки.

Основні Висновки по Прямим і ітераційних методів Рішення

Для вирішення систем лінійних рівнянь, що виникають при моделюванні, COMSOL автоматично підбере найкращий вирішувач без участі користувача. Прямі вирішувачі використовують більше пам'яті, ніж ітераційні, але при цьому мають більшою точністю (для коректно поставлених задач). Ітераційні вирішувачі наближаються до рішення поступово, і можна, за бажанням, змінювати відносну похибка рішення.