📌 Перша октава - це ... 🎓 Що таке Перша октава?

позначення октав
найменування октав
нотація Гельмгольца
наукова нотація
список октав [3]
контроктави
Велика октава
Мала октава
перша октава
друга октава
третя октава
четверта октава
п'ята октава
схема
Таблиця відповідності нот частотам
Див. також

Октавна система - спосіб угруповання і позначення музичних звуків на основі їх октавного подібності.

Музичні звуки, частота яких відрізняється в два рази сприймаються на слух як дуже схожі, як повторення одного звуку на різній висоті. Це явище має назву октавное схожість звуків. На основі цього весь діапазон частот використовуваних в музиці частот звуків ділиться на ділянки, звані октавами , При цьому частота звуків у кожній наступній октаві буде в два рази вище ніж у попередній, а схожі звуки отримують однакові назви ступенів .

Розташування частотних кордонів октав умовно і вибрано таким чином, щоб кожна октава починалася з першого ступеня ( « до ») Рівномірно темперованого двенадцатізвукового ладу і при цьому частота 6-го ступеня (« ля ») Однієї з октав (званої« першої ») становила б 440 Гц.

позначення октав

Діапазон застосовних в музиці звуків розбитий на 9 октав, кожна з яких має свою назву. Крім того існують різні способи позначення приналежності звуку тієї чи іншої октави, з яких найбільш поширені два - нотація Гельмгольца і наукова нотація.

найменування октав

Октава, що лежить посередині діапазону використовуваних в музиці звуків, називається «Перша октава», наступна вгору - «Друга», потім «Третя», «Четверта» і «П'ята». Октави нижче 1-й мають власні назви: «Мала октава» - це октава нижче 1-й, «Велика» - нижчу від мінімальної, «контроктави» - нижче великий і нарешті «субконтроктави» - нижче контроктави - найнижча з чутних октав. Октави нижче субконтроктави і вище 5-ї октави виходять за діапазон застосовуваних в музиці звуків і тому не мають власних назв і позначень звуків.

нотація Гельмгольца

Була запропонована німецьким математиком Германом Гельмгольцем в своїй роботі Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik (1863) [1] . Ця нотація заснована на комбінації способу запису назви ступені - з великою або маленькою літери, зокрема штрихів поруч з назвою ступені - від одного до п'яти (замість штрихів так само використовуються арабські цифри) і місця постановки штрихів - знизу або зверху. Нотація Гельмгольца може бути застосована як зі складової системою найменування ступенів, так і з буквеної.

наукова нотація

Другий спосіб позначення октав називається «наукова система позначення висоти звуку». Вперше була запропонована в 1939 році [2] Американським Акустичним Товариством. У науковій нотації номер октави записується відразу після позначення ступеня, при цьому октави нумеруються починаючи з найнижчої чутної (субконтроктави), якій присвоюється номер 0. Ця нотація застосовується тільки з буквеної системою найменування ступенів.

список октав [3]

субконтроктави

Включає звуки з частотами від 16.352 Гц (включно) до 32.703 Гц. Найнижча з чутних октав, як правило нижні щаблі цієї октави в музиці не використовуються. В нотації Гельмгольца найменування ступенів записуються з великої літери і праворуч знизу ставиться цифра 2 (або два штриха). У науковій нотації має номер 0.

контроктави

Включає звуки з частотами від 32.703 Гц (включно) до 65.406 Гц. В нотації Гельмгольца найменування ступенів записуються з великої літери і праворуч знизу ставиться цифра 1 (або один штрих). У науковій нотації має номер 1.

Велика октава

Включає звуки з частотами від 65.406 Гц (включно) до 130.81 Гц. В нотації Гельмгольца найменування ступенів записуються з великої літери без додаткових цифр або штрихів. У науковій нотації має номер 2.

Мала октава

Включає звуки з частотами від 130.81 Гц (включно) до 261.63 Гц. В нотації Гельмгольца найменування ступенів записуються з маленької літери без додаткових цифр або штрихів. У науковій нотації має номер 3.

перша октава

Включає звуки з частотами від 261.63 Гц (включно) до 523.25 Гц. Середня октава звукоряду музичної системи. В нотації Гельмгольца найменування ступенів записуються з маленької літери, справа зверху пишеться цифра 1 (або один штрих). У науковій нотації має номер 4.

друга октава

Включає звуки з частотами від 523.25 Гц (включно) до 1046.5 Гц. В нотації Гельмгольца найменування ступенів записуються з маленької літери, справа зверху пишеться цифра 2 (або два штриха). У науковій нотації має номер 5.

третя октава

Включає звуки з частотами від 1046.5 Гц (включно) до 2093.0 Гц. В нотації Гельмгольца найменування ступенів записуються з маленької літери, справа зверху пишеться цифра 3 (або три штриха). У науковій нотації має номер 6.

четверта октава

Включає звуки з частотами від 2093.0 Гц (включно) до 4186.0 Гц. В нотації Гельмгольца найменування ступенів записуються з маленької літери, справа зверху пишеться цифра 4 (або чотири штриха). У науковій нотації має номер 7.

п'ята октава

Включає звуки з частотами від 4186.0 Гц (включно) до 8372.0 Гц. Найвища з використовуваних в музиці октав, верхні щаблі застосовуються дуже рідко. В нотації Гельмгольца найменування ступенів записуються з маленької літери, справа зверху пишеться цифра 5 (або п'ять штрихів). У науковій нотації має номер 8.

схема

Таблиця відповідності нот частотам

Частоти в герцах (інтервал від середньої До в півтонах) Октава →
Нота ↓ 0 1 2 3 4 5 6 7 8 9 C 16.352 (-48) 32.703 (-36) 65.406 (-24) 130.81 (-12) 261.63 (0) 523.25 (+12) 1046.5 (+24) 2093.0 (+ 36) 4186.0 (+48) 8372.0 (+60) C # / Db 17.324 (-47) 34.648 (-35) 69.296 (-23) 138.59 (-11) 277.18 (+1) 554.37 (+13) 1108.7 (+25) 2217.5 (+37) 4434.9 (+49) 8869.8 (+61) D 18.354 (-46) 36.708 (-34) 73.416 (-22) 146.83 (-10) 293.66 (+2) 587.33 (+14) 1174.7 (+26 ) 2349.3 (+38) 4698.6 (+50) 9397.3 (+62) D # / Eb 19.445 (-45) 38.891 (-33) 77.782 (-21) 155.56 (-9) 311.13 (+3) 622.25 (+15) 1244.5 (+27) 2489.0 (+39) 4978.0 (+51) 9956.1 (+63) E 20.602 (-44) 41.203 (-32) 82.407 (-20) 164.81 (-8) 329.63 (+4) 659.26 (+16) 1318.5 (+28) 2637.0 (+40) 5274.0 (+52) 10548 (+64) F 21.827 (-43) 43.654 (-31) 87.307 (-19) 174.61 (-7) 349.23 (+5) 698.46 (+17 ) 1396.9 (+29) 2793.8 (+41) 5587.7 (+53) 11175 (+65) F # / Gb 23.125 (-42) 46.249 (-30) 92.499 (-18) 185.00 (-6) 369.99 (+6) 739.99 (+18) 1480.0 (+30) 2960.0 (+42) 5919.9 (+ 54) 11840 (+66) G 24.500 (-41) 48.999 (-29) 97.999 (-17) 196.00 (-5) 392.00 (+7) 783.99 (+19) 1568.0 (+31) 3136.0 (+43) 6271.9 ( +55) 12544 (+67) G # / Ab 25.957 (-40) 51.913 (-28) 103.83 (-16) 207.65 (-4) 415.30 (+8) 830.61 (+20) 1661.2 (+32) 3322.4 (+44 ) 6644.9 (+56) 13290 (+68) A 27.500 (-39) 55.000 (-27) 110.00 (-15) 220.00 (-3) 440.00 (+9) 880.00 (+21) 1760.0 (+33) 3520.0 (+ 45) 7040.0 (+57) 14080 (+69) A # / Hb 29.135 (-38) 58.270 (-26) 116.54 (-14) 233.08 (-2) 466.16 (+10) 932.33 (+22) 1864.7 (+34) 3729.3 (+46) 7458.6 (+58) 14917 (+70) H 30.868 (-37) 61.735 (-25) 123.47 (-13) 246.94 (-1) 493.88 (+11) 987.77 (+23) 1975.5 (+35 ) 3951.1 (+47) 7902.1 (+59) 15804 (+71)

Прим .: Іноді нота Сі-бемоль обзозначается як "B" замість "Hb".

Так само для знаходження частоти ноти можна користуватися нескладною формулою:

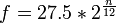(Гц), де n - це порядковий номер тону, починаючи з "ля" субконтр-октави, n відраховується з нуля.

Припустимо, нам потрібно знайти частоту "ре" малої октави. Підійдемо до піаніно і від самої лівої клавіші, починаючи рахувати з нуля, дізнаємося її порядковий номер. Це буде 29.

Отже,

Див. також

посилання

література

Способін Ігор Володимирович Елементарна теорія музики. - М .: Музика, 1968.
Тюлин Юрій Миколайович Короткий теоретичний курс гармонії. - М .: Музика, 1978.

Примітки

↑ Hermann von Helmholtz. (Nd). A Dictionary of Scientists. Retrieved April 15, 2008, from Answers.com Web site: http://www.answers.com/topic/hermann-von-helmholtz
↑ The Journal of the Acoustical Society of America - July 1939 - Volume 11, Issue 1, pp. 134-139
↑ Значення частот розраховані виходячи зі стандартної частоти камертона ля1 рівній 440 Гц

Wikimedia Foundation. 2010 року.