Закон рівномірної щільності ймовірності

3. Закон рівномірної щільності ймовірності.

Приклад. Похибка вимірювання напруги за допомогою вольтметра з дискретною шкалою (± (a - b) / 2 - половина поділу). МО є (a + b) / 2; дисперсія - (a - b) 2/12; середньоквадратичне відхилення (a - b) / (2 ).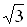

4. Нормальний (Гаусса) закон. Найпоширеніший в природі:

.

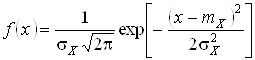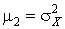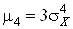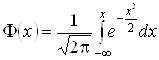Центральні моменти: ; ; ; і т.д. Отже, Sk = 0; Ex = 0. Для нормального закону при знаходженні ймовірності попадання випадкової точки на задану ділянку осі x є таблиці так званого інтеграла ймовірностей; їх кілька для різних виразів, наприклад: (Для m = 0 і s = 1). При визначенні ймовірності попадання на ділянку від а до b отримаємо . Інтерес для практики представляє визначення ймовірності попадання в інтервал, заданий в одиницях середньоквадратичного відхилення, наприклад, ± 3s. Так, наприклад, ця ймовірність є 0,997. Звідси випливає так зване «правило 3s». Для нормальних СВ це правило дозволяє на практиці наближено обчислювати s. Наприклад, при визначенні динамічного діапазону магнітофона за допомогою осцилографа при відсутності вольтметра.

Всі інші закони щільності ймовірності безперервних СВ утворені перетворенням рівномірного або нормального законів, наприклад:

- закон Сімпсона (трикутний). дисперсія 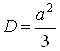. Згортка двох рівномірних законів відповідає щільності ймовірності суми двох незалежних рівномірно розподілених випадкових величин;

- закон Релея (корінь квадратний з суми квадратів двох СВ, розподілених за нормальним законом)

.

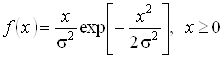Розподіл модуля комплексної випадкової величини при нормальних розподілах дійсної та уявної складових підпорядковується цим законом (розподіл обвідної вузькосмугового випадкового процесу).

Гістограма. По осі абсцис відкладаються розряди (інтервали шириною l), і на кожному з них як на підставі будується прямокутник, площа якого дорівнює частоті для даного розряду (оцінці ймовірності попадання значень в даний розряд - відношення числа влучень в розряд до загальної кількості випробувань). Для побудови гістограми потрібно частоту для кожного розряду розділити на його довжину і отримане число взяти в якості висоти прямокутника. Очевидно, що площа всіх прямокутників дорівнює

При збільшенні числа вимірювань N ширину l інтервалів можна зменшувати (збільшувати їх число m). У міру збільшення N і зменшення l гістограма буде наближатися до графіка щільності ймовірності величини X. Тобто гістограма є «портретом» щільності ймовірності. Для отримання «хорошого портрета» необхідно при заданому N раціонально вибрати число інтервалів. При малому числі інтервалів щільність ймовірності буде описуватися занадто грубо, у міру збільшення числа інтервалів буде виявлятися тонка структура щільності ймовірності. Але при занадто великій кількості інтервалів «портрет» знову істотно спотвориться: з'являться нерівномірності, що не закономірні для досліджуваної щільності ймовірності (в інтервали потрапить мало результатів вимірювань, і елемент випадковості призведе до спотворень).

Числові характеристики розподілу. Середнє арифметичне спостережуваних значень:

.

При збільшенні N статистичне середнє прагне до МО. Аналогічно оцінюється дисперсія - це середнє арифметичне квадрата центрованої СВ, тобто

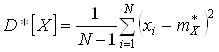, де .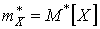

Таким же чином визначаються інші статистичні характеристики, наприклад: визначення щільності ймовірності по гістограмі.

Завдання це в значній мірі невизначена, так як складно підібрати щільність ймовірності, що відповідає моделі СВ, тобто виходячи з якого критерію можна гистограмму замінити підходящої щільністю ймовірності. Більш строго, але зі значними припущеннями вирішується ця проблема за допомогою критеріїв згоди, а зараз скористаємося простішими міркуваннями: спочатку виробляємо аналіз виду гістограми, порівнюючи її з відомими законами розподілу, а потім, підбираючи параметри цього закону, будемо домагатися найбільшого візуального подібності згладженої гістограми з кривою підібраною щільності ймовірності. Наприклад, якщо графік згладженої гістограми по виду близький до нормального закону, то розраховані за результатами вимірювань оцінки МО і 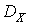можна використовувати для побудови нормальної щільності ймовірності і вважати її відповідної аналізованої вибірці СВ.

теорія ймовірності теорема дисперсія

бібліографічний список

1. Математичні основи сучасної радіоелектроніки [Текст] / І.А. Большаков [и др.]. - М.: Сов. радіо, 2009. - 208 с.

2. Гоноровський, І.С. Радіотехнічні ланцюги і сигнали [Текст] / І.С. Го-норовскій. - М.: Радио и связь, 2006. - 608 с.

1. Манжос, В.Н. Теорія і техніка обробки радіолокаційної інформа-ції на тлі перешкод [Текст] / Я.Д. Ширман, В.Н. Манжос. - М.: Радио и связь, 2011. - 416 с.

2. Фомічов, К.І. Моноімпульсна радіолокація [Текст] / А.І. Леонов, К.І. Фомічов. - М.: Сов. радіо, 2010. - 370 с.

3. Федосов, В.П. Статистична радіотехніка [Текст]: конспект лекцій / В.П. Федосов, В.П. Рижов. - Таганрог: Изд-во ТРТІ, 2008. - 76 с.

розділ: Комунікації і зв'язок
Кількість знаків з пробілами: 20614
Кількість таблиць: 1
Кількість зображень: 1

... шум). Відомо [2], що в таких умовах при вирішенні задачі виявлення критерієм якості роботи пристрою може служити відношення сигнал / перешкода, яке визначається трьома виразами: система випадкова величина відношення сигнал / перешкода за рівнем, де As - амплітуда сигналу; - дисперсія шуму; відношення сигнал / перешкода по потужності; енергетичне відношення сигнал / перешкода, де - енергія ...

... з дисперсією. Таблиця 3.1 Значення функції кореляції: j 1 2 3 4 5 6 7 8 9 10 R (j) -9.6 · 10-4 3.53 · 10-3 2.7 · 10-4 4.24 · 10-3 -1.73 · 10-3 6.61 · 10-4 4.11 · 10-4 6.74 · 10-5 3.95 · 10-4 1.12 · 10-3 Завдання 4. Виконати моделювання випадкової величини, розподіленої за законом Релея. Обсяг вибірки n = 17, s2 = 27. Рішення Ддя ...

... -ним законом розподілу ширини щілин і стінок може бути представ-лен наступним виразом: (2.16). Найбільший інтерес для практичної реалізації в оптичних системах КОС для автоматизації контролю статистичних характеристик просторової структури ЛЗ представляє другий доданок вираження (2.16), що містить функціональну взаємозв'язок цих характеристик. Пос-кольку це доданок ...

... Глава II. Методики дослідження забруднення навколишнього середовища і оцінки її якості Для виконання завдань та досягнення мети були розроблені нами методики дослідження комплексної еколого-геохімічної оцінки урболандшафтами Волгоградської агломерації, яка полягає в дослідженні грунтів, рослинності, оцінки викидів промислових підприємств і впливу ОС на здоров'я людини. 2.1 ...