Застосування методу Монте-Карло для оптимізації торгових стратегій

1. Зміст Загальна теорія
2. Імовірнісна модель радника
3. застосування теорії
4. Стійкість прибутку до випадкового розкиду
5. Стійкість прибутку до просідання
6. Стійкість розподілу прибутку угод до нестаціонарності цін
7. Висновок
8. вкладені файли

Зміст

Загальна теорія

суть методу Монте-Карло можна описати як приклад використання аналогії - одного з методів наукового пізнання. Інші приклади аналогії - оптико-механічна аналогія Гамільтона в фізиці або аналогічні органи в біології.

Якщо у нас є два об'єкти, які можна описати однією і тією ж теорією, то знання, отримані при вивченні одного з них, будуть застосовні і до іншого. Цей метод дуже корисний, коли вивчити один об'єкт набагато простіше, ніж інший. Тоді більш доступний для вивчення об'єкт вважається моделлю іншого, а сам метод називається моделюванням . Іноді моделлю (або теоретичною моделлю) називають не один з об'єктів, а загальну для них теорію, але зазвичай з контексту ясно, про що саме йде мова.

Іноді дослідники невірно сприймають результати моделювання. Коли мова йде про очевидні прикладах - наприклад, про обдув зменшеної копії літака в аеродинамічній трубі, то все здається очевидним. Коли ж об'єкти не пов'язані і не схожі один на одного на перший погляд, то висновки часом здаються якимось хитрим трюкацтвом або ж служать основою для необґрунтованих, але далекосяжних висновків і узагальнень. Насправді справа в тому, що загальна для об'єктів теорія завжди тільки приблизно описує лише їх деякі аспекти. Чим менше необхідна нами точність опису об'єктів теорією, тим ширше безліч об'єктів, які будуть їй підкорятися. Наприклад, оптико-механічна аналогія Гамільтона точно виконується лише в межі, при прагненні довжини світлової хвилі до нуля. У реальності тільки для малої, але завжди кінцевої довжини вона виконується лише приблизно. Оскільки будь-яка теоретична модель повинна бути досить простий, щоб служити основою для розрахунків і висновків, то вона завжди буде огрубіння.

Уточнимо тепер поняття методу Монте-Карло. Це підхід до моделювання об'єктів, теорія яких має вірогідну (стохастичну) природу. Моделлю при цьому служить комп'ютерна програма, алгоритм якої влаштований в Відповідно до цієї теорії. У ній використовуються генератори псевдовипадкових чисел, щоб імітувати необхідні випадкові величини (випадкові процеси) з необхідними розподілами.

Варто підкреслити (хоча для подальшого нашого викладу це і неважливо), що природа досліджуваного об'єкта може бути і ймовірнісної, і детермінованою. Важливо лише, щоб для нього існувала теорія, що має імовірнісний характер. Наприклад, метод Монте-Карло використовується для наближеного підрахунку звичайних інтегралів. Це можливо, тому що будь-який такий інтеграл можна розглядати як математичне очікування деякої випадкової величини.

Першим прикладом використання методу Монте-Карло зазвичай вважається рішення завдання Бюффона, в якому число Пі визначається за допомогою випадкового кидання голки на стіл. Назва методу з'явилося набагато пізніше, в середині XX століття. Адже всі азартні ігри - наприклад, рулетка - це генератори випадкових чисел. Плюс до всього, свідома відсилання до азартних ігор натякає на витоки теорії ймовірностей, яка починалася з обчислень, пов'язаних з грою в кості й карти.

Алгоритм програми для моделювання простий, і це одна з причин поширеності методу. У ній випадковим чином, з розподілом, відповідним теорії, генерується безліч різних варіантів (семплів) стану досліджуваного об'єкта. Для кожного з них розраховується необхідний набір характеристик. В результаті виходить велика вибірка. У той час, як для досліджуваного об'єкта у нас є тільки єдиний набір характеристик, метод Монте-Карло дає нам можливість отримати їх у великій кількості і побудувати функції їх розподілу, що дає нам набагато більше інформації.

Загальна схема моделювання Монте-Карло, описана вище, здається простою. Але при її реалізації на практиці виникає безліч різних, іноді дуже складних варіацій. Навіть якщо обмежитися застосуванням в області фінансів, то можна переконатися, наскільки воно широко - наприклад з цієї книги . Ми спробуємо застосувати метод Монте-Карло для вивчення стійкості торгових радників. Для цього нам потрібна імовірнісна модель, що описує їх роботу.

Імовірнісна модель радника

Перед тим, як почати реальну торгівлю з використанням радника, ми зазвичай тестуємо і оптимізуємо його на історії котирувань. Виникає резонне питання: чому ми вважаємо, що результати торгівлі в минулому визначають їх в майбутньому? Природно, ми не чекаємо, що всі угоди в майбутньому утворюють абсолютно ту ж послідовність, що і в минулому. Але припущення про деяку їх "схожості" у нас, очевидно, є. Формалізуємо це інтуїтивне уявлення про "схожості", використовуючи теорію ймовірностей. Відповідно до цієї формалізацією, ми вважаємо, що результат кожної операції - конкретна реалізація деякої випадкової величини. "Схожість" угод в цьому випадку визначається через близькість відповідних їм функцій розподілу. У такій формалізації угоди, вчинені в минулому, допомагають уточнити вид розподілу для майбутніх угод і судити про їх можливі результати.
В рамках ймовірнісної формалізації можна будувати різні теорії. Розглянемо найпростішу і найбільш часто використовувану. У ній результат кожної угоди однозначно визначається відносною прибутком k = C 1 / C 0, де C 0 та C 1 - обсяг капіталу до і після операції. Надалі відносну прибуток угоди будемо називати просто прибутком, а різниця C 1-C 0 - абсолютної прибутком угоди. Припустимо, що прибули всіх угод (як в минулому, так і в майбутньому) спільно незалежні і однаково розподілені випадкові величини. Їх розподіл визначається функцією розподілу F (x). Таким чином, перед нами стоїть завдання визначити вид цієї функції, використовуючи значення прибутків угод з минулого. Це стандартна задача математичної статистики - відновлення функції розподілу за вибіркою. Будь-які способи її вирішення завжди дають наближені відповіді. Уявімо деякі з цих способів.

1. Як наближення використовується емпірична (вибіркова) функція розподілу .

2. Береться просте дискретний розподіл, при якому прибуток угоди приймає одне з двох значень. Це або середній збиток з ймовірністю збитку, або середній прибуток з ймовірністю прибутку.

3. Будується не дискретне, а безперервне (має щільність) наближення для функції розподілу. Для цього використовуються методи на кшталт ядерної оцінки щільності .
   

Надалі ми будемо використовувати перший варіант - він найпростіший і універсальний. Трейдеру не дуже цікаво знати саму функцію. Важливо знати, які величини вказують на можливий прибуток від роботи радника, на ризикованість його використання або на стійкість прибутку. І ці величини можна отримати, знаючи функцію розподілу.
Конкретизуємо алгоритм моделювання в нашому випадку. Що нас цікавить об'єкт - можливий результат роботи радника в майбутньому. Він однозначно задається послідовністю операцій. Кожна угода задається значенням прибутку. Прибутки розподілені відповідно до описаного вище емпіричним розподілом. Ми повинні згенерувати велику кількість таких послідовностей і підрахувати для кожної з них необхідні характеристики. Генерація кожної такої послідовності влаштована просто. Позначимо послідовність прибутків угод, отриманих на історії, через k 1, k 2, ..., kn. Генеруючи послідовності довжиною N, будемо N раз вибирати випадковим чином (з однаковою ймовірністю 1 / n) одне з ki (вибірка з поверненням). Зазвичай вважають N = n, оскільки при великих N точність наближення F (x) емпіричним розподілом падає. Цей варіант методу Монте-Карло іноді називають методом бутстрапа.

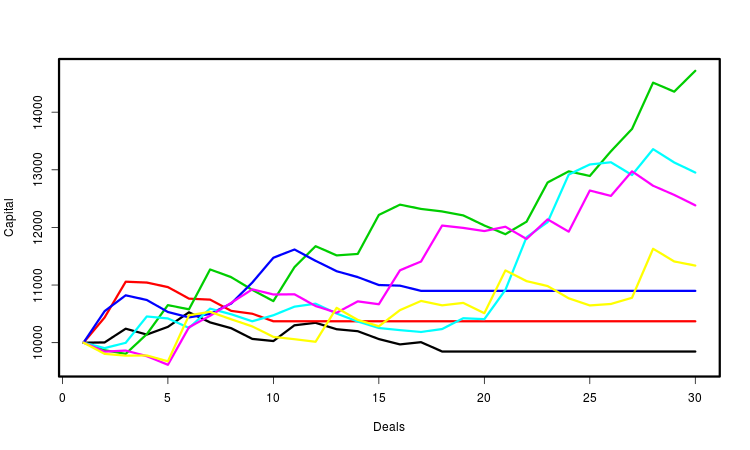
Пояснимо вищесказане малюнком. На ньому зображено кілька кривих капіталу, кожна з яких визначається згенерованої послідовністю операцій. Для зручності сприйняття я позначив їх різними кольорами. Насправді їх число набагато більше - кілька десятків тисяч. Для кожної з них ми обчислюємо необхідні характеристики і робимо статистичні висновки на основі їх сукупності. Очевидно, найважливіша з таких характеристик - це кінцевий прибуток.

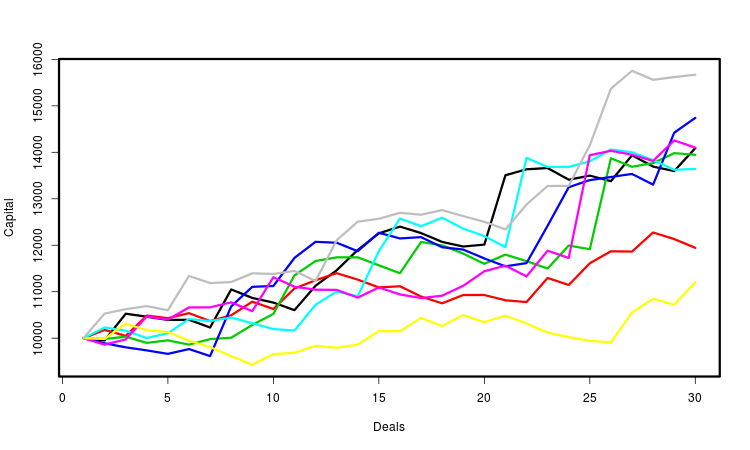
Можливі й інші підходи до імовірнісної формалізації і подальшого моделювання роботи радника. Наприклад, замість послідовностей угод можна моделювати послідовності цін і вивчати сукупність прибутків, які радник на них отримав. Принцип генерації цінових рядів можна буде підібрати в залежності від того, яке завдання потрібно вирішити. Але цей метод потребує набагато більшої кількості обчислювальних ресурсів. До того ж, в даний час в MetaTrader немає регулярних способів використовувати його для довільного радника.

застосування теорії

Наше завдання - побудувати конкретні критерії оптимізації. Кожен з них відповідає певній меті, головна з яких - кінцева прибуток, отриманий в результаті всієї серії угод. Оптимізація по ній вбудована в тестер. Але оскільки нам цікава прибуток в майбутньому, то ми повинні якось оцінити можливу ступінь її відхилення від прибутку в сьогоденні. Чим менше це відхилення, тим стійкіше прибуток системи. Розглянемо три підходи.

1. Отримавши за допомогою методу Монте-Карло велику вибірку можливих значень прибутку, можемо вивчити її розподіл і пов'язані з ним величини. Дуже важливо середнє значення цього прибутку. Важлива і дисперсія - чим вона менша, тим стійкіше робота радника і менше невизначеність в майбутніх його результатах. Наш критерій буде дорівнює відношенню середньої прибутку до її середньому розкиду. Він схожий на коефіцієнт Шарпа.
2. Інша важлива характеристика - просадка прибутку в серії угод. Занадто велика просадка може привести до втрати депозиту, навіть якщо радник прибутковий. З цієї причини на просідання зазвичай накладається обмеження. Корисно знати, як воно впливає на можливий прибуток. Критерій визначено просто як середня прибуток, але з умовою, що моделюється припинення торгівлі при перевищенні допустимого рівня осідання.

3. Побудуємо критерій, що вимірює стійкість прибутку в плані сталості розподілу прибутків угод. З точки зору теорії ймовірності, це означає стационарность прибутків угод, яка, в принципі, можлива і в разі нестаціонарності збільшень ціни. Для цього ми скористаємося ідеєю, схожою на форвард-тестування. Розіб'ємо вихідну вибірку угод на початкову і кінцеву підвибірки. Для перевірки їх однорідності ми можемо застосувати будь-якої статистичний тест. На підставі такого тесту ми і створимо умов для оптимізації.
   

Для демонстрації нашої теорії скористаємося радником «Moving Average.mq5», що входить в поставку MetaTrader 5. внесемо в його код невеликі зміни. На початок радника додамо рядок коду для включення нашого заголовки:
#include <mcarlo.mqh>

В кінець радника додамо код отримання і використання нашого оптимизационного параметра:

double OnTester () {return optpr (); }

Основні обчислення відбуваються у функціях, які знаходяться в заголовки «mcarlo.mqh». Його ми поміщаємо в папку «MQL5 / Include /». Основна функція в цьому файлі - optpr (). При виконанні необхідних умов вона обчислює заданий параметром noptpr варіант оптимізаційного критерію, а інакше повертає нуль.

double optpr () {if (noptpr <1 || noptpr> NOPTPRMAX) return 0.0; double k []; if (! setks (k)) return 0.0; if (ArraySize (k) <NDEALSMIN) return 0.0; MathSrand (GetTickCount ()); switch (noptpr) {case 1: return mean_sd (k); case 2: return med_intq (k); case 3: return rmnd_abs (k); case 4: return rmnd_rel (k); case 5: return frw_wmw (k); case 6: return frw_wmw_prf (k); } Return 0.0; }

Функція setks () обчислює масив прибутків угод, виходячи з історії торгівлі.

bool setks (double & k []) {if (! HistorySelect (0, TimeCurrent ())) return false; uint nhd = HistoryDealsTotal (); int nk = 0; ulong hdticket; double capital = TesterStatistics (STAT_INITIAL_DEPOSIT); long hdtype; double hdcommission, hdswap, hdprofit, hdprofit_full; for (uint n = 0; n <nhd; ++ n) {hdticket = HistoryDealGetTicket (n); if (hdticket == 0) continue; if (! HistoryDealGetInteger (hdticket, DEAL_TYPE, hdtype)) return false; if (hdtype! = DEAL_TYPE_BUY && hdtype! = DEAL_TYPE_SELL) continue; hdcommission = HistoryDealGetDouble (hdticket, DEAL_COMMISSION); hdswap = HistoryDealGetDouble (hdticket, DEAL_SWAP); hdprofit = HistoryDealGetDouble (hdticket, DEAL_PROFIT); if (hdcommission == 0.0 && hdswap == 0.0 && hdprofit == 0.0) continue; ++ nk; ArrayResize (k, nk, NADD); hdprofit_full = hdcommission + hdswap + hdprofit; k [nk- 1] = 1.0 + hdprofit_full / capital; capital + = hdprofit_full; } Return true; }

Функція sample () генерує випадкову послідовність b [] з вихідної послідовності a [].

void sample (double & a [], double & b []) {int ner; double dnc; int na = ArraySize (a); for (int i = 0; i <na; ++ i) {dnc = MathRandomUniform (0, na, ner); if (! MathIsValidNumber (dnc)) {Print ( "MathIsValidNumber (dnc) error", ner); ExpertRemove ();} int nc = (int) dnc; if (nc == na) nc = na- 1; b [i] = a [nc]; }}

Далі ми докладно розглянемо кожен з трьох вищевказаних видів оптимізаційних критеріїв. У всіх випадках оптимізувати будемо на одному і тому ж часовому інтервалі - весна / літо 2017 роки для EURUSD. Таймфрейм завжди буде 1 годину, а режим тестування - OHLC з хвилинного графіка. Завжди буде використовуватися генетичний алгоритм по кастомними критерієм оптимізації. Оскільки наше завдання - демонстрація теорії, а не підготовка радника до реальної торгівлі, то такий спрощений підхід здається цілком природним.

Стійкість прибутку до випадкового розкиду

Припустимо, що у нас є вибірка з згенерованих кінцевих прибутків. Ми можемо вивчати її за допомогою методів математичної статистики. На малюнку нижче побудована гістограма і пунктирною лінією вказана вибіркова медіана.

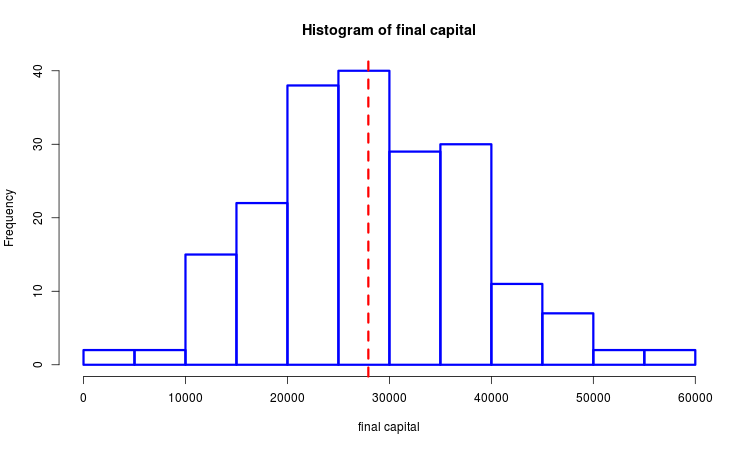
Побудуємо два схожих варіанту оптимізаційного критерію. Вони обчислюються у функціях mean_sd () і med_intq (). Загальна в цих варіантах - то, що вони представляють собою відношення середнього до міри розкиду. Відмінність - в тому, як визначено середнє і міра розкиду. У першому випадку це середнє арифметичне і середнє квадратичне відхилення, а в другому - вибіркові медіана і інтерквартільний розмах . Обидва вони тим більше, чим більше прибуток і чим менше її розкид. Є очевидна схожість з коефіцієнтом Шарпа, тільки тут мова йде про прибуток у всій серії угод, а не в одній угоді. Другий варіант критерію більш стійкий до викидів, у порівнянні з першим.

double mean_sd (double & k []) {double km [], cn [NSAMPLES]; int nk = ArraySize (k); ArrayResize (km, nk); for (int n = 0; n <NSAMPLES; ++ n) {sample (k, km); cn [n] = 1.0; for (int i = 0; i <nk; ++ i) cn [n] * = km [i]; cn [n] - = 1.0; } Return MathMean (cn) / MathStandardDeviation (cn); } Double med_intq (double & k []) {double km [], cn [NSAMPLES]; int nk = ArraySize (k); ArrayResize (km, nk); for (int n = 0; n <NSAMPLES; ++ n) {sample (k, km); cn [n] = 1.0; for (int i = 0; i <nk; ++ i) cn [n] * = km [i]; cn [n] - = 1.0; } ArraySort (cn); return cn [(int) (0.5 * NSAMPLES)] / (cn [(int) (0.75 * NSAMPLES)] - cn [(int) (0.25 * NSAMPLES)]); }

Нижче показані дві пари результатів тестування радників, оптимізованих за цим критерієм. На першій парі - результат оптимізації за першим варіантом і, для порівняння, результат з максимальним прибутком. Очевидно, що перший з них краще, оскільки дає більше гладку криву капіталу. Кінцевий прибуток при бажанні можна збільшити, збільшивши обсяг угод.

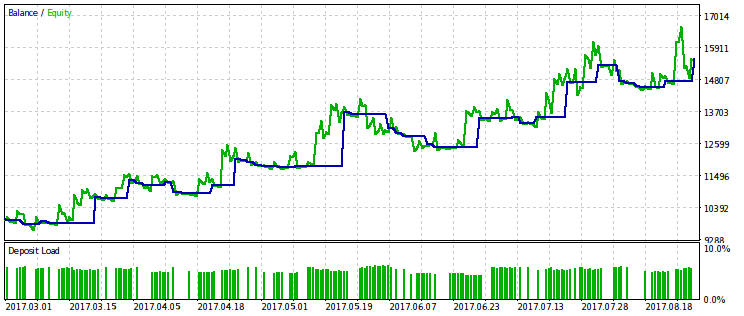
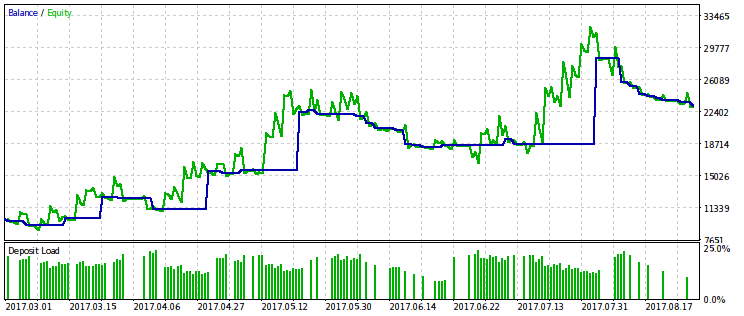
Така ж пара результатів наведена для другого варіанту оптимізаційного критерію. По ній можна зробити такі ж висновки.

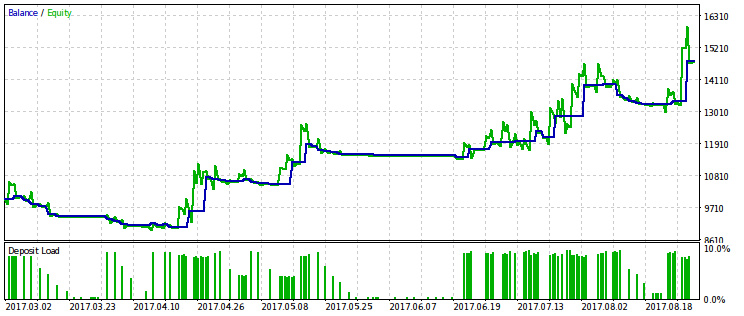
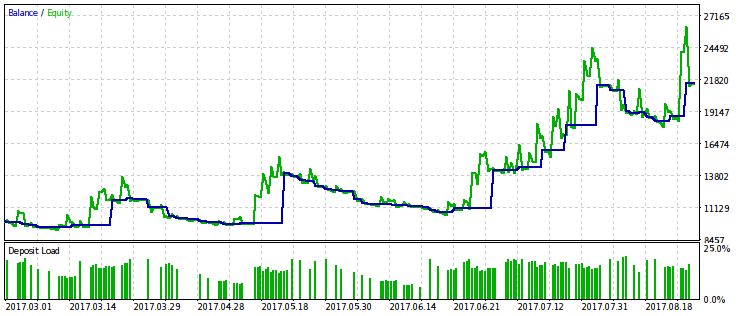
Стійкість прибутку до просідання

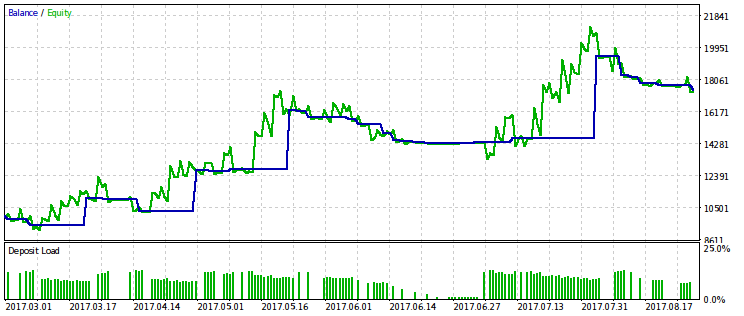
У кожній згенерувала угод ми стежимо за величиною осідання. Якщо залишок капіталу після початкової частини серії угод становить меншу частку, ніж задано параметром rmndmin, то залишилися угоди відкидаються. На малюнку нижче можна побачити, що в разі перевищення рівня відносної просадки капітал перестає змінюватися, і кінцевий ділянку лінії капіталу стає горизонтальним.

У нас є два варіанти розрахунку критерію - для абсолютної і відносної просадки. У разі абсолютної просадки частка капіталу вважається від його початкового значення, а в разі відносного - від максимального. Функції, що обчислюють ці варіанти параметрів, називаються, відповідно, rmnd_abs () і rmnd_rel (). В обох випадках значення критерію - це середнє згенерованих прибутків.

double rmnd_abs (double & k []) {if (rmndmin <= 0.0 || rmndmin> = 1.0) return 0.0; double km [], cn [NSAMPLES]; int nk = ArraySize (k); ArrayResize (km, nk); for (int n = 0; n <NSAMPLES; ++ n) {sample (k, km); cn [n] = 1.0; for (int i = 0; i <nk; ++ i) {cn [n] * = km [i]; if (cn [n] <rmndmin) break; } Cn [n] - = 1.0; } Return MathMean (cn); } Double rmnd_rel (double & k []) {if (rmndmin <= 0.0 || rmndmin> = 1.0) return 0.0; double km [], cn [NSAMPLES], x; int nk = ArraySize (k); ArrayResize (km, nk); for (int n = 0; n <NSAMPLES; ++ n) {sample (k, km); x = cn [n] = 1.0; for (int i = 0; i <nk; ++ i) {cn [n] * = km [i]; if (cn [n]> x) x = cn [n]; else if (cn [n] / x <rmndmin) break; } Cn [n] - = 1.0; } Return MathMean (cn); }

Ми можемо проводити оптимізацію або з відповідним фіксованим параметром rmndmin, або шукати його оптимальне значення.

Наведемо результати лише для критерію, пов'язаного з відносною осіданням, оскільки її обмеження дає більш виражений ефект. Проведемо оптимізацію з декількома варіантами фіксованого значення rmndmin: 0.95, 0.75 і 0.2.

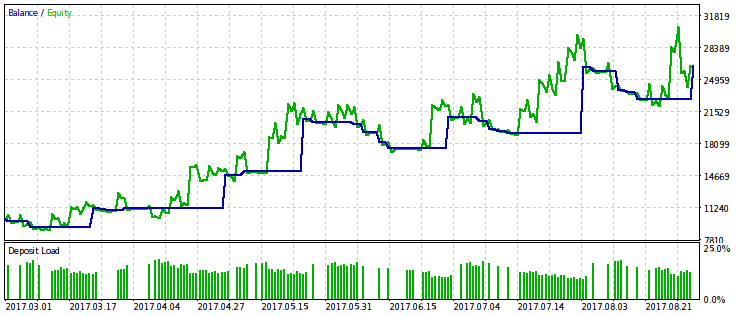
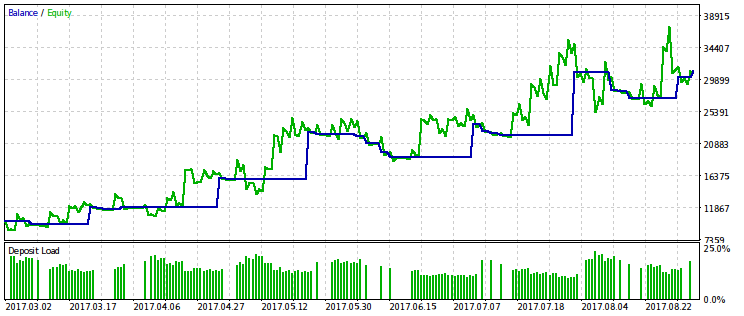
Чим менше значення rmndmin, тім Менш помітно обмеження по просідання, и результати оптімізації все більш схожі на Такі при звічайній максімізації прибутку. Це можна вважаті наслідком закону великих чисел - принципу Теорії ймовірностей. На малюнках цею ефект НЕ відразу помітній, оскількі на них різний масштаб по вертікальній осі (через підгонкі всех малюнків до однакової розмірах) и не відразу очевидними є зростання просадки при зменшенні rmndmin.
Тепер включимо параметр rmndmin в число оптимізуються і продовжимо оптимізацію за тим же критерієм.

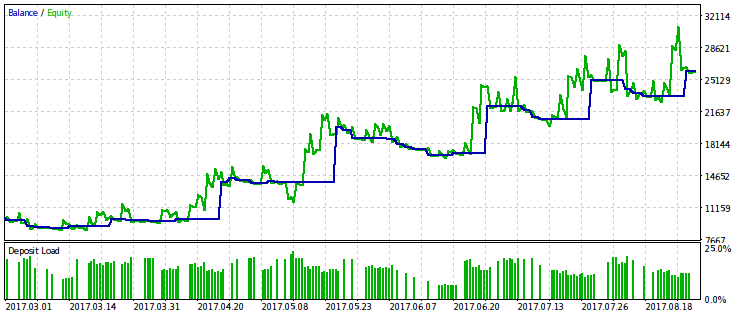
Отримаємо оптимальне значення rmndmin = 0.55. При такому його значенні ми готові до просідання майже на половину рахунку, що виглядає малоприйнятною. Тому навряд чи варто використовувати його в реальній торгівлі. Користь тут в іншому - видно, що "пересиджування" ще більших просадок, швидше за все, не має ніякого сенсу. Це відповідає другій половині приказки: "Дозволяй прибутку рости, обрізай збитки".

Стійкість розподілу прибутку угод до нестаціонарності цін

Поведінка цін може змінюватися. При цьому хотілося б, щоб результати роботи радника були стабільними. З точки зору нашої ймовірнісної моделі радника це означає, що нам потрібна стационарность прибутків угод навіть у разі нестаціонарності збільшень ціни.
Наш критерій оптимізації порівнює початкову частину послідовності операцій з кінцевою, і чим вони ближче, тим його значення більше. Близькість визначається на основі критерію Уилкоксона-Манна-Уїтні . Пояснимо його суть. Нехай у нас є дві вибірки з угод. Критерій визначає, наскільки сильно зрушена одна щодо іншої. Чим менше зрушення, тим вище значення критерію. Пояснимо це малюнком: на ньому кожна вибірка представлена ​​відповідною їй гистограммой. Найбільше значення критерію спостерігається на середньому малюнку.

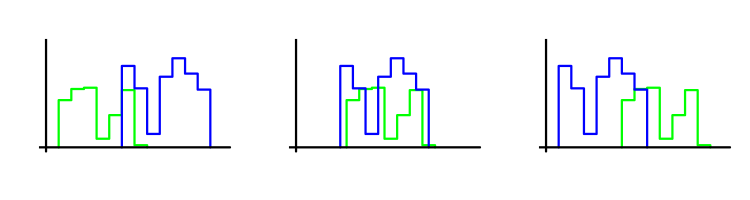
У цьому випадку сам по собі метод Монте-Карло не використовується. Однак велика величина WMW-критерію служить обгрунтуванням для його застосування, оскільки підтверджує припущення про те, що вид розподілу прибутків угод зберігається.
У нашому файлі є й інший варіант критерію - твори WMW-критерію на прибуток.

double frw_wmw (double & k []) {if (fwdsh <= 0.0 || fwdsh> = 1.0) return 0.0; int nk = ArraySize (k), nkf = (int) (fwdsh * nk), nkp = nk-nkf; if (nkf <NDEALSMIN || nkp <NDEALSMIN) return 0.0; double u = 0,0; for (int i = 0; i <nkp; ++ i) for (int j = 0; j <nkf; ++ j) if (k [i]> k [nkp + j]) ++ u; return 1.0 -MathAbs (1.0 -2.0 * u / (nkf * nkp)); } Double frw_wmw_prf (double & k []) {int nk = ArraySize (k); double prf = 1.0; for (int n = 0; n <nk; ++ n) prf * = k [n]; prf- = 1.0; if (prf> 0.0) prf * = frw_wmw (k); return prf; }

WMW-критерій безпосередньо використовувати проблематично, тому що він може прийняти збитковий варіант за оптимальний. Краще було б оптимізувати радник по прибутку і відкидати варіанти з невеликим значенням цього параметра, але поки незрозуміло, як це зробити. Можна вибирати якусь кількість найкращих з точки зору WMW-критерію варіантів, а потім вибирати з них той, який дає максимальний прибуток.

Наведемо приклади двох з десяти найкращих проходів. Один буде прибутковим, а інший - збитковим.

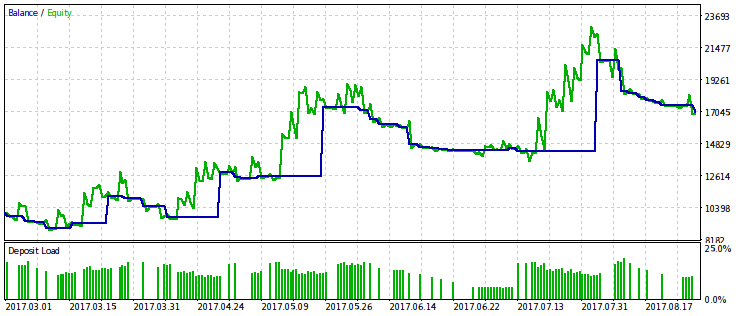
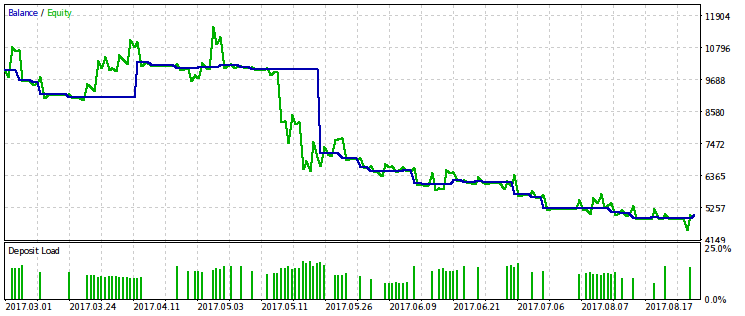
Створюється враження, що WMW-критерій був би більш корисний при порівнянні двох різних радників на одному і тому ж часовому проміжку або одного і того ж радника на різних. Але поки незрозуміло, як зробити таке порівняння регулярним.

Також наведемо приклад оптимізації за критерієм, рівному твору WMW-критерію на прибуток. Судячи з усього, вона дуже схожа на просту оптимізацію по прибутку, а значить, її застосовувати буде надмірно.

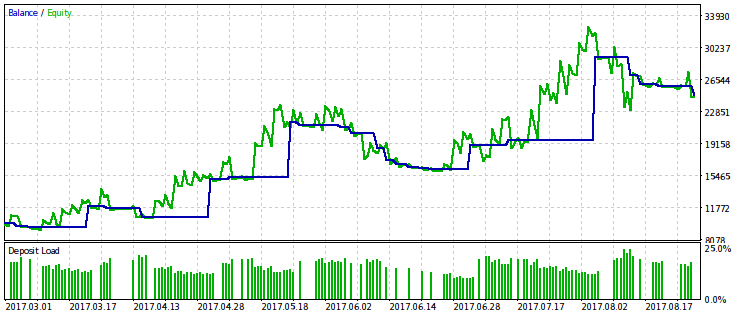
Висновок

У даній статті ми лише трохи лише торкнулися деяких аспектів означеної теми. Завершимо її короткими зауваженнями.

• Побудовані в статті критерії оптимізації можуть бути корисні при формалізації інтуїтивних уявлень про те, яка послідовність операцій краще. Це корисно при виборі з великого числа варіантів.
  
• Є відомі заходи для ризику, на зразок VaR (Value At Risk) або ймовірності розорення. Якщо їх використовувати безпосередньо в якості критерію для оптимізації, то результат буде неважливим. Обсяги торгівлі і кількість угод будуть заниженими. Тому потрібен компромісний критерій, який залежить від двох змінних - і від ризику, і від прибутку. Проблема в тому, який саме варіант цього критерію вибрати, оскільки функцій від двох змінних нескінченно багато. Вибір критерію, наприклад, може визначатися рівнем "агресивності" торгової стратегії, яка дуже сильно варіюється.
  
• Для різних класів радників можуть бути корисні різні варіанти критеріїв оптимізації, що вимірюють стійкість. Наприклад, трендові радники будуть відрізнятися від торгуючих в діапазоні, а системи з фіксованим тейк-профітом будуть відрізнятися від закривають угоди по трейлинг-стопу. Розподілу прибутків таких радників теж будуть належати різним класам, і в залежності від цього буде більш підходящим той чи інший критерій.
• Деякі критерії корисні не стільки для порівняння поведінки одного і того ж радника на фіксованому проміжку часу при різних наборах параметрів, скільки для порівняння двох різних радників. За допомогою таких критеріїв можна порівнювати і роботу одного радника на різних часових проміжках.
  
• Моделювання методом Монте-Карло було б більш повним, якби була можливість подавати на вхід радника не тільки наявну історію цін, але і її копії, змінені випадковим чином. Це дозволило б вивчати стійкість радників більш грунтовно, хоча і ціною збільшення обсягу обчислень.
  

вкладені файли

№
имя
тип опис
1
Moving Average_mcarlo.mq5 Скрипт
Модифікований стандартний Moving Average.mq5 2
mcarlo.mqh Заголовний файл
Основний файл з функціями, які виконують всі необхідні обчислення